 Тем, кто ищет, где в интернете купить дешевый китайский ширпотреб, лучше сразу направиться на АлиЭкспресс. Часто одни и те же китайские продавцы торгуют одинаковыми товарами на разных площадках, включая онлайн-аукцион eBay. Данную статью я написал, чтобы помочь русскоязычным пользователям интернета в поисках тех товаров, которых нет на AliExpress, JD.com и в других китайских интернет-магазинах. Мощным конкурентным преимуществом онлайн-аукциона ебей является большой выбор там настоящих брендовых вещей, коллекционных и винтажных товаров, антиквариата, предлагаемых продавцами со всего мира.
Тем, кто ищет, где в интернете купить дешевый китайский ширпотреб, лучше сразу направиться на АлиЭкспресс. Часто одни и те же китайские продавцы торгуют одинаковыми товарами на разных площадках, включая онлайн-аукцион eBay. Данную статью я написал, чтобы помочь русскоязычным пользователям интернета в поисках тех товаров, которых нет на AliExpress, JD.com и в других китайских интернет-магазинах. Мощным конкурентным преимуществом онлайн-аукциона ебей является большой выбор там настоящих брендовых вещей, коллекционных и винтажных товаров, антиквариата, предлагаемых продавцами со всего мира.
Годами функционеры eBay улаживали споры с правообладателями брендов, их производителями, параллельно вычищая аукцион от торговцев контрафактом, подделками под продукцию известных брендов. Была введена строгая система рейтингов для оценки продавцов ебей, сняты риски с покупателей за счет 100% гарантийного покрытия от PayPal на случаи утери товара при почтовой пересылке или мошенничества со стороны продавцов. Теперь покупатель на онлайн-аукционе ебей всегда прав в любом случае. Купить на eBay подделку у продавца с длительной торговой историей и высокими позитивными фидбэками на данный момент практически нереально. Модницам и модникам на заметку: особенно активно на eBay ведется торговля следующими брендами: Ann Taylor, Banana Republic, DKNY, Eileen Fisher, J Crew, Lucky Brand, Michael Kors, Vince, Tory Burch, Ralph Lauren. Полный список брендов одежды, обуви и сумок, разрешенных правообладателями для продаж на ебей, смотрите на специальной, постоянно обновляемой страничке на сайте онлайн-аукциона. Там же находится приблизительная прикидка средних цен на товары упомянутых марок.
Ниже привожу таблицу с перечислением лучших eBay-магазинов. По каким критериям составлена данная подборка, я подробно описал под таблицей. В подборке представлены магазины, предлагающие самые разнообразные товары: от норковых шуб и оригинальных сумок Биркин из кожи крокодила до автомобилей Porsche, от игрушечных радиоуправляемых вертолетов до тайского шелка и японских кимоно, от недорогих произведенных в Китае купальников до антиквариата из Европы и предметов живописи.
eBay- | Товары |
|---|---|
Антиквариат и этнические товары |
|
i.sell.my. | Датский фарфор Royal Copenhagen и винтажные товары, художественная керамика и декоративные металлические изделия, христианское искусство. |
tomo | Инструменты для японских чайных церемоний, традиционная ручная работа, японский антиквариат. |
Africa Direct  | Африканское искусство: африканские маски, статуэтки, ткани с традиционным орнаментом, корзины, этнические ювелирные украшения, африканская каменная скульптура шона, а также тибетские ювелирные изделия. |
Brian Di | Редкие, коллекционные книги и старинные карты на английском языке. |
Magic Rugs Outlet  | Восточные ковры, персидские ковры, ковры современных дизайнов. |
Искусство |
|
ArtGate- | Европейская живопись маслом. |
Uncle Terry's Treasures  | Разнообразный антиквариат. |
Art Com | Живопись, принты, фотографии, скульптура. |
Gallery Art Florida Aventura  | Живопись современных американских художников от Энди Уорхола до Роберта Индианы. |
Фото и видео |
|
irohas camera  | Фотоаппараты и аксессуары из Японии. |
A-Plus ANIME CAMERA CONNECT  | Широкий выбор цифровых фотоаппаратов и фотоаксессуаров. |
Teds Electronics  | Зеркальные фотоаппараты и аксессуары к ним. |
photo | Антикварные и винтажные коллекционные фотоаппараты. |
Мобильные телефоны и аксессуары |
|
Simply | Новые и б/у мобильные телефоны и аксессуары к ним. В магазине представлено также множество других гаджетов. |
imkt | Б/у айфоны (Apple iPhone) и смартфоны Самсунг (Samsung). |
always-for-you  | Широкий выбор чехлов для смартфонов и планшетов. |
Diamond Wire | Оптовые предложения мобильных телефонов и аксессуаров. |
GSM | Б/у мобильные телефоны и аксессуары. |
Одежда, обувь и аксессуары |
|
Gigi's Classy Kids  | Детская одежда и обувь. |
Chinese | Традиционная китайская одежда для мужчин и женщин. |
Japan Expo Store  | Кимоно и большой выбор других традиционных японских товаров. |
Sweden Luxury Sales  | Магазин, торгующий оригиналами Hermes Birkin, Hermes Constance других культовых женских сумок. Цены высокие. |
Mode | Шведский онлайн-бутик, специализирующийся на брендовой одежде Dolce & Gabbana. |
fashion from uk Boutique  | Британский магазин, торгующий женской дизайнерской одеждой, обувью и аксессуарами CHANEL, DIOR, YSL, GUCCI, PRADA, HERMES и других производителей. Этот eBay-магазин отсылает заказы из Лондона. |
Pelgio Leather  | Изделия из экзотических кож: сумки из кожи крокодила, крокодиловые кошельки, ремни, шкуры крокодила; шкуры морского ската, кожа змеи и страуса. Сумки, ремни, кошельки из кожи ската, питона, акулы и страуса. Товар произведен в Таиланде. |
Dilart Plus UG  | Женские шубы из Германии. Мех: шиншилла, рысь, белка, норка, лиса, песец. |
MAILON FURS  | Широкий выбор шуб для женщин и мужчин, произведенных в Греции. |
Vanity Affair Boutique  | Предметы из коллекций haute couture для дам, следящих за последними тенденциями высокой моды. |
Mono | Женские сумки Louis Vuitton б/у из Японии. |
Newmart  | Женская брендовая обувь и сумки. |
Bag Lady Collection  | Женские оригинальные сумки MICHAEL KORS и других модных брендов. |
Eve-Sher Fashion Con | Брендовая женская обувь и сумки. Хорошо представлены Fendi, Dior, Jimmy Choo, Nina Ricci, Chloe, Gucci, Yves Saint Laurent, Givenchy, Prada, Dolce & Gabbana и изделия иных модных брендов. |
BEAUTI | Одежда для беременных. |
The Eye Shop  | Большой выбор солнцезащитных очков. |
sghstock  | Женская и мужская обувь. |
Tough | Ковбойская обувь и одежда для мужчин, женщин и детей. Почувствуй себя американским фермером. |
Galindas- | Большой выбор оригинальных джинсов Levi's для мужчин. |
Hawaii | Красочные гавайские рубашки. |
KICK | Спортивная обувь, включая культовые кроссовки Nike Air Max. |
Retail | Стильные кожаные кошельки из Великобритании. |
Millian Dresses UK  | Свадебные и вечерние платья. |
frmoda- | Брендовая женская одежда, обувь и аксессуары следующих марок: Gucci, Prada, Dolce & Gabbana, Hogan, Church, Burberry, Dsquared, Tod's, Fendi, Moncler, Jimmy Choo, Givenchy, Lanvin, Armani и др. |
WyCo Vintage  | Винтажные футболки. |
VTGDR  | Недорогая мужская одежда из Китая. |
luvlabels  | Люксовая дизайнерская одежда, обувь и аксессуары из Великобритании под брендами Christian Louboutin (мечта модниц - туфли лабутены), Givenchy, Burberry, Jimmy Choo, MONCLER, Miu Miu, Vivienne Westwood. |
usa | Мужская и женская одежда и обувь для активного образа жизни. |
Arura Clothing  | Одежда и обувь марок Diesel, True Religion, Adidas, Puma, Nike, Reebok, Polo Ralph Lauren, The North Face, Asics, Jordan, Lacoste, Under Armour, Wilson. |
Shop Smart 500  | Женская, мужская и детская обувь. |
BELLE LINGERIE  | Женское нижнее белье и купальники из Великобритании. |
james | Мусульманская одежда для женщин. |
Компьютеры, планшеты и компьютерное "железо" |
|
INTECH | Компьютеры,ноутбуки,планшеты и компьютерные комплектующие. |
deecies  | Ноутбуки Apple MacBook и моноблоки Apple iMac с доставкой из Великобритании. |
Daily | Айфоны и айпады (Apple iPads/iPhones), смартфоны и планшеты Samsung Galaxy. |
hello | Китайские смартфоны и планшеты Xiaomi, Huawei, Lenovo, Asus. Для тех, кому привычнее покупать китайские товары на Алиэкспресс: официальный магазин Xiaomi на AliExpress. |
COMPEVE  | Десктопы, серверы и компьютерные комплектующие. |
Swing Computers  | Ноутбуки Apple MacBook, моноблоки Apple iMac, компактные компьютеры Apple Mac mini. Большой выбор ноутбуков Dell, HP, MSI. |
Acooinc Store  | Блоки питания для ноутбуков, компьютерное "железо" для ноутбуков, нетбуков и планшетов. |
beach | Компьютеры и комплектующие, бытовая электроника и офисные принадлежности, включая расходные материалы (картриджи/тонеры) для принтеров. |
Inter | Лицензионный софт для компьютеров. |
Красота и здоровье |
|
COSME | Косметика и парфюмерия из Великобритании. |
carol | Японская и французская косметика. |
Alpha Beauty Store  | Огромный выбор японской косметики с доставкой из Гонконга. |
skinstory  | Корейская косметика и парфюмерия из Южной Кореи. |
Euro Glamour Zone  | Духи из Европы. |
Authentic Vintage Perfumes  | Аутентичный винтажный парфюм. |
Hannari- | Косметика для настоящих японских гейш. |
Ювелирные изделия и часы |
|
Kampfer Uhren  | Немецкий eBay-магазин с большим выбором швейцарских часов. |
Time | Часы Stuhrling, Invicta, Michael Kors, DKNY, Fossil, Eterna, Haurex, Swiss Military и др. |
JJ Around the Clock  | Солнцезащитные очки и часы Guess, Fossil, Nixon, DKNY, DIESEL, ARMANI, CASIO, Philippe Starck, Maui Jim, Ray Ban, зажигалки Zippo. |
La Jolla Jewelry  | Часы и ювелирные изделия Rolex, Cartier, Breitling, Van Cleef & Arpels, Tiffany & Co, Baccarat, Bvlgari, Lalique, Audemars Piguet, Patek Phillipe, Jeager LeCoultre, Vacheron Constantin. |
Watch | Ювелирные изделия и часы с бриллиантами от Rolex, Breitling, Cartier, Joe Rodeo. |
Wahenoor | Драгоценные камни из Индии: рубины, сапфиры, изумруды, жемчуг, аквамарины, турмалины. |
thai | Драгоценные камни из Таиланда: аметисты, бриллианты, изумруды, рубины, сапфиры, топазы. |
Спорт и рыбалка |
|
MuayThai Fighting  | Товары для муай тай (тайского бокса) от TUFF, Top King, Twins Special, Kombat Gear, Hanumann, Fairtex и других производителей. |
Forza Sports  | Спортивная одежда, обувь и снаряжение. |
Orge Bike Shop  | Запасные части для велосипедов, карбоновые велосипеды из Китая. |
Colorado Discount Skis  | Лыжи и лыжные крепления из Колорадо следующих марок: Atomic, Stockli, Fischer, Elan, Ogasaka. |
Asian | Рыболовные снасти из Японии. |
Fishwest  | Снасти и принадлежности для рыбной ловли нахлыстом. |
The Golf Avenue  | Большой выбор клюшек и мячей для гольфа. |
Racket | Всё для тенниса: ракетки, мячи, сумки, обувь. |
Автомобили, мотоциклы, яхты |
|
mmgcars  | Американский автодилер из Флориды с большим выбором новых и подержанных автомобилей. В этом магазине часто выставляются подержанные электромобили Тесла по интересным ценам. |
Auto Gallery Chicago  | Подержанные автомобили Porsche, Jaguar, Tesla, Volvo, BMW, Audi, Aston Martin, Bentley, Maserati, Mercedes, Ferrari, Lexus, Infiniti. |
primo | Классические авто, олдтаймеры (старинные, раритетные автомобили) из США. |
AM AutoParts  | Автозапчасти и комплектующие для легковых автомобилей и грузовиков. |
American Classic Motors  | Подержанные мотоциклы Harley-Davidson, Kawasaki, Yamaha, Honda. |
GJM COMBO  | Одежда, обувь, шлемы, перчатки для байкеров. |
Race Leathers  | Британский магазин, торгующий одеждой, обувью, шлемами, перчатками и прочими причиндалами для байкеров. |
Boats Inter | Катера и яхты. |
Rocky Mountain RV  | Дома на колесах (автодома) для путешествий с домашним комфортом. |
Еда и напитки |
|
it.factory | Зеленый чай, улун, пуэр и разнообразные травяные чаи из Китая. |
cosmetics japan  | Японский зеленый чай из Японии: сентя, кукича, фукамуши сенча, маття. |
TeaCakes of Yorkshire  | Различные виды чая из Великобритании. |
Fresco Gourmet Coffee  | Кофе и чай из Великобритании. |
Jamaican Favorite  | Ямайский кофе Blue Mountain и различные традиционные средства для красоты и здоровья с острова Ямайки. |
easy | Кофе и средства традиционной медицины на основе трав из Индонезии. |
Всякая всячина |
|
RC Hobby Experts  | Радиоуправляемые вертолеты-игрушки и детали для них. |
Swords | Японские мечи, изготовленные в Японии. Катана, вакидзаси, тати (еще называют тачи или дайто), цуба, традиционные японские ножи танто (последние служили для отрезания человеческих голов или харакири, а не для бытовых нужд) и камни для заточки мечей. |
Nancy Botwins  | Швейцарские ножи Victorinox и американские зажигалки Zippo. |
YuiSenri  | Японские кухонные ножи. |
Bangkok | Тайский шёлк, сатин и другие ткани из Бангкока. |
Bay Trade Japan  | Японские традиционные чашки для чая, инструменты для чайной церемонии, ножи сакаи такаюки и другие традиционные японские товары. |
Ellai Baba | Индийская косметика, специи и аюрведические товары. |
Kmise Musical Instrument  | Аутлет музыкальных инструментов от китайской фабрики: укулеле, банджолеле и детали для них. |
Nikitov | Семена овощей, цветов, табака, споры грибов от продавца из Украины. |
panto | Семена кактусов и других комнатных растений от энтузиастов из Италии. |
Критерии для отбора популярных eBay-магазинов:
- Feedback > 97%, также желателен высший статус продавца — top-rated seller;
- Более 1000 листингов выставлено на продажу;
- Есть eBay-магазин у продавца;
- Регистрация аккаунта на онлайн-аукционе до 2016 года;
- Отправка товаров по всему миру или в большое количество стран
Сам, будучи продавцом на eBay под разными аккаунтами c 2003 года, могу сказать, что фидбэк продавца на ебей (количество отзывов) — это очень важный критерий оценки качества его работы. Алгоритм подсчета фидбэков очень прост: от количества позитивных отзывов отнимается количество негативных отзывов, а затем результат делится на общее количество отзывов. Процент позитивных отзывов у продавца на ебэй, как лакмусовая бумажка, позволяет гипотетическим покупателям быстро принять решение, связываться ли с ним или искать других продавцов. В идеале у продавца должно быть 100% позитивных отзывов. Не спешите ставить продавцу негативный отзыв! Возможно, ваш заказ затерялся где-то на местной почте. В случае форс-мажора просто откройте диспут (dispute — это спор, если по-русски) в своем аккаунте. Многие продавцы будут готовы пойти на полное возмещение заплаченных за заказ денег, чтобы избежать получения негативных отзывов. Обращайте внимание также на внутренний рейтинг продавца. Для оценки качества продавцов онлайн-аукцион использует хитрый алгоритм, присваивающий продавцу рейтинг. Рейтинги бывают следующие: below average (ниже среднего), average (средний), above average (выше среднего) и самый высокий — top rated seller. Последний получить непросто. Строгие алгоритмы eBay требуют от продавца, чтобы подавляющее большинство проданных товаров отправлялось на почте в день получения платежа или на следующий рабочий день. Оценивается качество и быстрота работы с диспутами, оперативность ответов на запросы пользователей, наличие бесплатной доставки (как правило, продавцы просто включают ее в стоимость товара) и другие факторы.
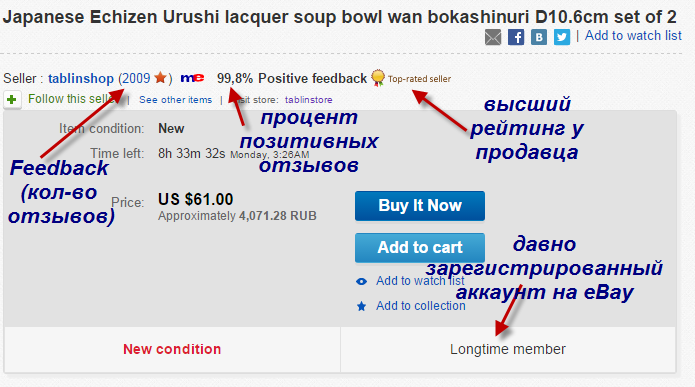 Интуитивно понятная схемка, на что смотреть в описании товара на ебей, чтобы оценить продавца: общее количество отзывов (feedback), процент позитивных отзывов, значок top rated seller’а и отметка о том, что аккаунт на аукционе зарегистрирован давно.
Интуитивно понятная схемка, на что смотреть в описании товара на ебей, чтобы оценить продавца: общее количество отзывов (feedback), процент позитивных отзывов, значок top rated seller’а и отметка о том, что аккаунт на аукционе зарегистрирован давно.
Теперь обсудим второй критерий — количество выставленных листингов. Общее правило, чем оно больше, тем лучше, так как больше товаров. Обычно один листинг — один товар. Но есть исключения: в виде одного листинга на ебей нередко оформляют продажу большого количества однотипных товаров, особенно с функцией Buy It Now (мгновенная покупка и оплата, без режима аукциона). Например, Apple iPhone/iPad или компьютерные детали. Все реже на ибэй можно встретить голландские аукционы. Иногда в виде одного листинга оформляют несколько товаров разного цвета и/или размеров. Например, одежду или сумки одной модели, но разных цветов. А теперь я попытаюсь проиллюстрировать ниже, почему листинги листингам рознь. И почему второй пункт о 1000 и более листингах в одном eBay-магазине — это желательный пункт.
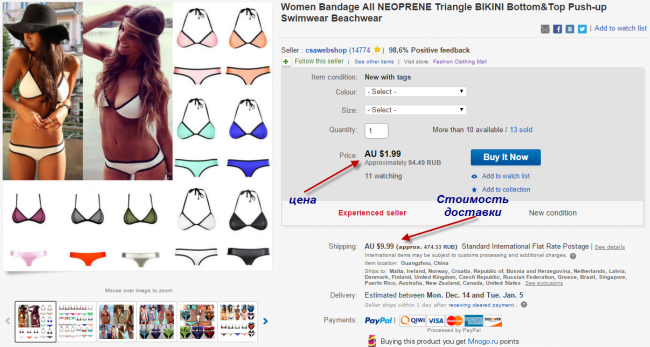 Вот китайский магазин на eBay, торгующий женскими купальниками. Продавец использует старинную китайскую хитрость: ставит на сам товар заниженную цену, зато свою прибыль извлекает за счет стоимости почтовой доставки. Все равно купальник обойдется дешево: в 570 рублей вместе с доставкой.
Вот китайский магазин на eBay, торгующий женскими купальниками. Продавец использует старинную китайскую хитрость: ставит на сам товар заниженную цену, зато свою прибыль извлекает за счет стоимости почтовой доставки. Все равно купальник обойдется дешево: в 570 рублей вместе с доставкой.
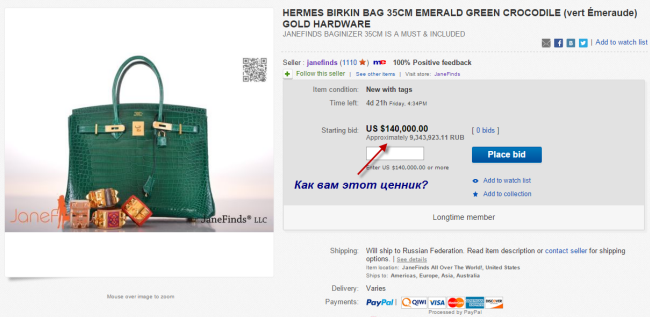 А вот, например, ценник на оригинальную сумку Hermes Birkin из кожи крокодила изумрудно-зеленого цвета в магазине eBay, специализирующемся на женских сумках Hermes, поставлен на космическом уровне в 140 тысяч долларов США.
А вот, например, ценник на оригинальную сумку Hermes Birkin из кожи крокодила изумрудно-зеленого цвета в магазине eBay, специализирующемся на женских сумках Hermes, поставлен на космическом уровне в 140 тысяч долларов США.
Понятно, что поставить торговаться на аукционе 1000 женских купальников себестоимостью производства в Китае в 5 долларов и 1000 настоящих сумок Hermes Birkin из кожи крокодила — это не одно и то же. Кстати, и позитивный отзыв за купальник, и позитивный отзыв за сумку Биркин — номинально это + 1 к фидбэку. Но сколько контейнеров купальников нужно продать, чтобы получить такую же выручку, как за одну сумку из примера выше?
Третий критерий — наличие, собственно, eBay-магазина. Может показаться странным, но я находил множество продавцов на ебей, выставляющих тысячи листингов с товарами, но без своего магазина. Товары крутятся в общей базе аукциона, торговля идет. eBay-магазин позволяет позиционировать свой товар более удобным образом. Короткую ссылку на магазин удобно использовать для привлечения интернет-трафика с помощью контекстных и медийных объявлений в сети или соц.сетях. Да, eBay-магазин в базовом пакете будет стоить продавцу $19,99 в месяц, но комфорт того стоит.
Четвертый критерий — это как давно аккаунт на eBay был зарегистрирован. Необязательно сразу для торговли. Многие нынешние продавцы на eBay были там сначала покупателями. Хотя я находил некоторых деятелей, которые торгуют на eBay с 1998 года, то есть всего на три года позже основания этой компании (1995). Общее правило: чем более старый аккаунт у продавца, тем лучше.
Пятый критерий — Worldwide Delivery, то есть отправка товаров по всему миру. Большое количество американских магазинов на eBay специализируются на продаже товаров внутри США. Америка — это большой рынок. Эти продавцы не хотят брать риски почтовой доставки в другие страны мира или связываться с иностранными покупателями-мошенниками или с кардерами, покупающими товар по украденным данным кредитных карточек. К сожалению, у многих подобных американских продавцов наблюдается обилие качественных товаров по интересным ценам. Но в моей подборке лучших магазинов eBay давать на них ссылки не имеет смысла, так как эта информация не будет полезной для читателей моего блога. Я старался выбирать магазины с почтовой доставкой по всему миру, ну, или в большое количество стран мира. Часто продавцы на eBay исключают страны Африки и Афганистан из списка стран, куда возможна доставка заказов. Очень плохая репутация у стран в этих регионах планеты, а платежеспособный спрос их жителей находится под большим вопросом. Продавцы предпочитают просто не связываться.
Что делать, если продавец на eBay отсылает заказы только по США, а вещь купить хочется?
Есть три варианта:
- Убедить продавца выслать вам товар в вашу страну. Метод срабатывает примерно в 20% случаев. Торговец заинтересован продать свой товар быстро и по хорошей цене. Напишите продавцу на eBay сообщение на английском языке о том, что хотите приобрести этот товар, готовы заплатить по PayPal максимально быстро. Поинтересуйтесь, может ли он послать товар в вашу страну и сколько это будет стоить. Правда, если у вас как у покупателя на ебей нулевой фидбэк (то есть, вы ничего на этом онлайн-аукционе раньше не покупали), то шансы убедить продавца сделать исключение из его правил по доставке заказов будут стремиться к нулю.
- Обратиться к посреднику — компании, которая специализируется на доставке покупок в интернет-магазинах США в вашу страну. Компания за определенную комиссию купит на eBay, Amazon или во многочисленных американских интернет-магазинах понравившуюся вам вещь, примет посылку с ней на адрес своего склада в Америке, а потом перешлет посылку из США на ваш адрес в родной стране. Можно комбинировать несколько онлайн-покупок из разных магазинов в одну посылку, чтобы экономить на международной почтовой доставке. За сервис посредника придется заплатить сверху, но часто дополнительные траты оказываются оправданными. Принимайте решение, исходя из своей собственной ситуации. Выгодны ли вам услуги посредника или нет?
- Найти аналогичный товар в местных магазинах или на других онлайн-площадках.
Если речь идет о произведенных в Китае товарах, то смысла заказывать их с eBay нет. Попробуйте найти аналоги в магазинах на Алиэкспресс. Благо дело, там представлено более 200 тысяч китайских продавцов.
Если нужен брендовый товар, а не китайская подделка, но на eBay нет продавцов, отсылающих его за пределы Америки, поищите на Амазон. Какой-то конкретный известный бренд? Обязательно должен быть официальный интернет-магазин, торгующий изделиями под этим брендом. Google вам в поиск. В России искать товары в онлайн-магазинах и сравнивать цены на них удобно с помощью сервиса Яндекс.Маркет.
Как покупать на eBay.com. Видео-руководство от опытного онлайн-покупателя.
Множество интересных магазинов есть на немецком eBay. Это целый мир шоппинга в немецкоязычном интернете. Я не стал включать немецкие eBay-магазины в данную подборку, так как для eBay Germany планирую сделать отдельный рейтинг. Также я отфильтровал eBay-магазины, где много категорий товаров. В этом они похожи на универмаги. Очень сложно рекомендовать такие магазины на eBay, так как покупателю там очень непросто сфокусировать внимание на чем-то одном. Если читателю интересен онлайн-шоппинг широкого профиля, то я бы посоветовал ему/ей обратить свой взор на отечественные интернет-магазины Озон.ру и Юлмарт.
На аукционе ебей представлено море интересных и необычных товаров. Сам я просто физически не в состоянии просмотреть всё. Добавляйте в комментариях ниже ссылки на другие понравившиеся магазины eBay, которых нет в списке выше, приводите ссылки на товары. Похвастайтесь покупками, либо пожалуйтесь на продавца, чей товар не оправдал ожиданий. Может быть, вам интересны какие-то конкретные товары, а я забыл их упомянуть? Напишите в комментариях ниже. Я с удовольствием добавлю в список eBay-магазины, которые подходят под вышеописанные критерии.
Данная статья доступна также и на других языках: английском, испанском, португальском (бразильская версия), французском, немецком, тайском, китайском, индонезийском, вьетнамском, японском, арабском.





